来自 Yi Zou | February 3, 2020
按:本系列文章的第三篇,本来计划介绍一下新型冠状病毒的疫情时间序列的可视化,碰巧收到了西交利物浦大学邹怡博士的投稿。他利用 logistic 模型,预测了新型冠状病毒全国疫情的结束时间。利用 R 语言进行拟合的简介,可以参看《学R》第四章。
准备工作:
运行下面的代码,将 “ncovr” 包升级到 0.0.3 以上:
remotes::install_github("pzhaonet/ncovr")下面是邹怡博士的投稿,略有改动。
请记住:每一个数据背后,都是一个鲜活的生命。
模型目的:看疫情什么时候结束
数据来源:卫健委全国每日数据,也可以从 https://github.com/JackieZheng/2019-nCoV 的图中读取
第1步,数据的获取。 ncovr 包的 get_ncov() 可以从上述网址读取数据表:
Sys.setlocale('LC_CTYPE', 'Chinese')## [1] "Chinese (Simplified)_China.936"require(ncovr)
ncov <- get_ncov('china')
ncov## 日期 确诊 疑似 重症 死亡 治愈 确认+疑似 新增(疑似+确认) 观察中
## 1 2020-01-20 291 54 NA 6 25 345 NA 922
## 2 2020-01-21 440 37 102 9 28 477 132 1394
## 3 2020-01-22 571 393 95 17 49 964 487 4928
## 4 2020-01-23 830 1072 177 25 34 1902 938 8420
## 5 2020-01-24 1287 1965 237 41 38 3252 1350 13967
## 6 2020-01-25 1975 2684 324 56 49 4659 1407 21556
## 7 2020-01-26 2744 5794 461 80 51 8538 3879 30453
## 8 2020-01-27 4515 6973 976 106 60 11488 2950 44132
## 9 2020-01-28 5974 9239 1239 132 103 15213 4904 59990
## 10 2020-01-29 7711 12167 1370 170 124 19878 4665 81947
## 11 2020-01-30 9692 15238 1527 213 171 24930 5052 102427
## 12 2020-01-31 11791 17988 1795 259 243 29779 4849 118478
## 13 2020-02-01 14380 19544 2110 304 328 33924 4145 137594
## 14 2020-02-02 17205 21558 2296 361 475 38763 4839 152700
## 15 2020-02-03 NA NA NA NA NA NA NA NA
## 更新时间 备注
## 1 2020/1/21 截至1月20日24时
## 2 2020/1/22 截至1月21日24时
## 3 2020/1/23 截至1月22日24时
## 4 2020/1/24 截至1月23日24时
## 5 2020/1/25 截至1月24日24时
## 6 2020/1/26 截至1月25日24时
## 7 2020/1/27 截至1月26日24时
## 8 2020/1/28 截至1月27日24时
## 9 2020/1/29 截至1月28日24时
## 10 2020/1/30 截至1月29日24时
## 11 2020/1/31 截至1月30日24时
## 12 2020/2/1 截至1月31日24时
## 13 2020/2/2 截至2月1日24时
## 14 2020/2/3 截至2月2日24时
## 15这个数据表最早的数据是 1 月 20 日。为了增加和验证模型的可靠性,我们手动录入了 1 月 17 日至 19 日的的确诊病例、疑似病例和死亡病例数据,并取 1 月 17 日至 2 月 1 日的数据做回归分析:
Confirmed <- c(58, 136, 198, ncov[1:13, '确诊'])
Suspected <- c(NA, NA, NA, ncov[1:13, '疑似'])
Death <- c(1, 1, 4, ncov[1:13, '死亡'])第2步,把数据合成数据框,方便操作
Dat <- data.frame(Confirmed, Death, Suspected)
# 设置一列为时间
Dat$Date <- seq(as.Date("2020-01-17",format="%Y-%m-%d"),
by = "day",
length.out = nrow(Dat))
# 以1月17日作为第一天,是x变量
Dat$Day <- 1:nrow(Dat)第3步,做logistic回归,这里采用的是三参的logistic非线性回归,模型是 y~Asym/(1+exp((xmid-input)/scal))。其中input(x)是我们的Day。Asym是模型渐近线,xmid是中值(y=1/2*Asym时候x的值)。这是一个简单的模型,模型的合适程度在这里就不讨论了。
# 选择模型的y,我们先以确诊病例作为y
Dat$Ymod <- Dat$Confirmed
#模型需要设置初始值,但是我们也可以采用自动初始值用SSlogis()函数
md <- nls(Ymod ~ SSlogis(Day, Asym, xmid, scal), data = Dat)
Coe <- summary(md)$coefficients
a <- Coe[1, 1]# 第一个参数Coe[1,1]是模型渐近线
xmax <- 2 * Coe[2, 1] #第二个参数Coe[2,1]是模型x中值第4步,我们可以把回归的图画出来。
#先画散点图
with(Dat,
plot(y = Ymod, x = Day,
xlim = c(0, 1.8 * xmax),
ylim = c(0, 1.2 * a),
ylab = "Number of cases",
xlab = "",
bty = 'n',
xaxt = "n"
)
) #用xaxt = "n"先隐藏x轴
#模型的预测值和预测线
Pred <- seq(0, 1.2 * xmax, length = 100)
lines(Pred, predict(md, list(Day = Pred)), col = "red")
#画上x轴
Length <- round(2.2 * nrow(Dat), 0)#需要预测到第几天,这里采用2.2倍的我们的数据时间
Dseq <- format(seq(Dat$Date[1], by = "day", length.out = Length), "%m-%d") #设置新的x轴标签
axis(1, at = 1:Length, labels = Dseq,
cex.axis = 0.6,las = 2)
#做一个简单的图例,当然也可以用legend做图例
points(2, 0.8 * a)
text(3, 0.8 * a, "Confirmed", cex = 0.8, adj = 0)
segments(1.5, 0.7 * a, 2.5, 0.7 * a, col = "red")
text(3, 0.7 * a, "Model fit", cex = 0.8, adj = 0)
#画上两条参考线
segments(0, a, xmax, a, lty = "dotted")
segments(xmax, 0, xmax, a, lty = "dotted")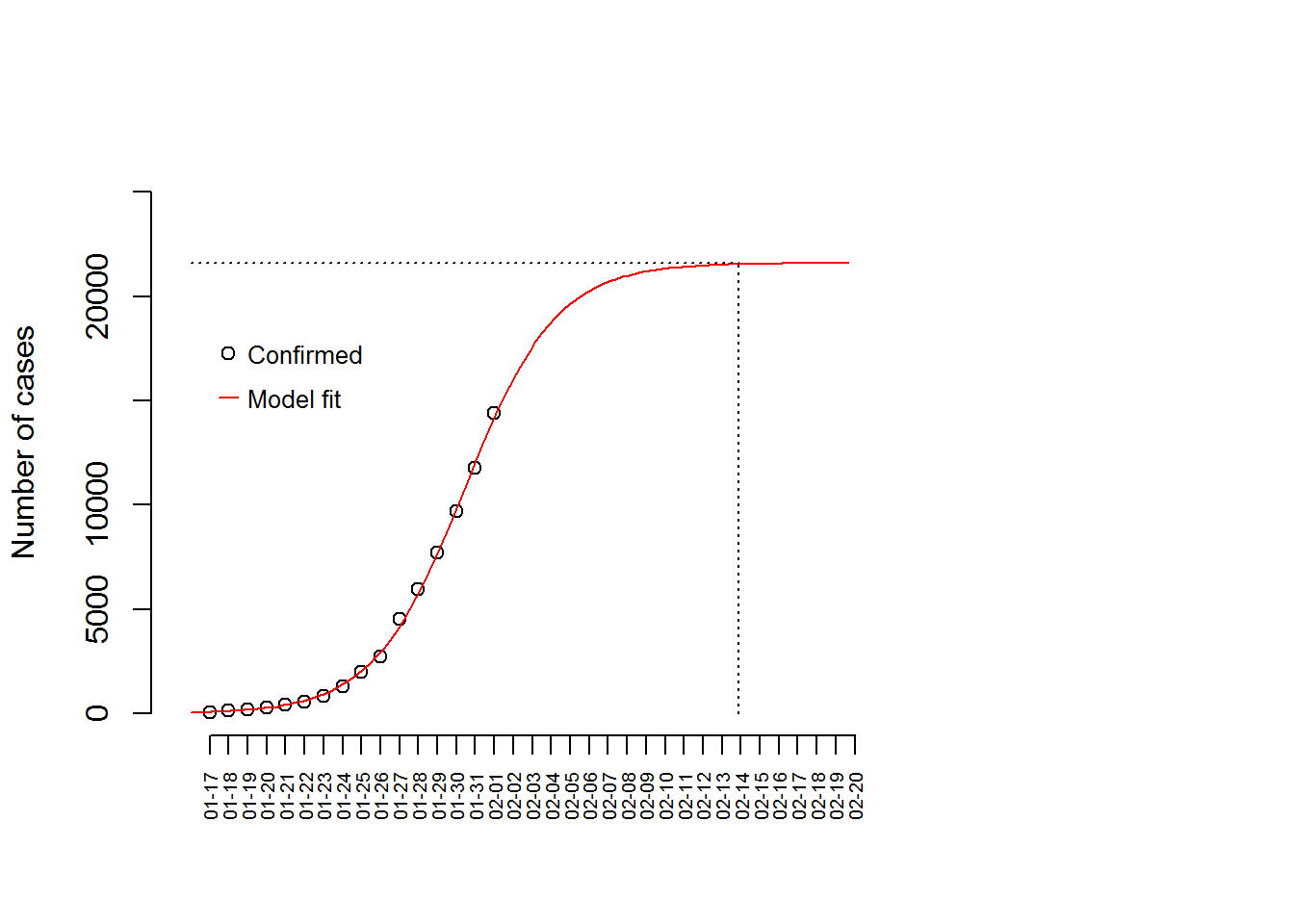
第四步接下来是重点,根据模型,我们来估计疫情大致结束的时间(双倍的中值,即xmax)
Dseq [round(xmax,0)]## [1] "02-14"2月14日!不算太糟糕,根据这个模型,我们预计下一天(2月3日)早的确诊病例
Input = nrow(Dat) + 1
Coe[1, 1] / (1 + exp((Coe[2, 1] - Input) / Coe[3, 1]))## [1] 16054.01数值是16054个。今天早上我查了相关的数据,是17205,比预测值高。我们可以把这个数值加进去,重复1-4步的操作,得出来的时间是2月16号,比先前的模型预测又推迟了两天。
进一步的思考:
1、疑似病例
确诊病例可能受到资源不足(比如试剂盒)的影响,其增长是因为前期疑似病例无法及时确诊,所以我们可以用疑似病例作为y,重新做一下上面的模型。得出的结论是2月11号,并没有增加太多,算是个好兆头。
2、地方的情况
湖北的疑似病例也可能受到资源不足的影响而整体有积压,我们可以做一个湖北以外的省份的模型。由于数据量比较大,我们可以直接联网获取各个地区的数据(见上一篇文章),看看各个地区的形式。
最后,再次提醒:每一个数据背后,都是一个鲜活的生命。希望疫情早日结束,我们可以进入正常的工作和生活中。

